# Side channel : l'attaquant est pas sur le réseau mais chez Alice !!!
Raison des side channels :
- Cloud
- Logiciel malveillant
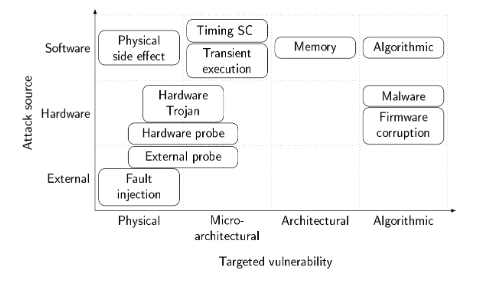
**Architecture** : ce qu'un utilisateur peut voir facilement : un attaquant utilise les informations connues du système
👉️ Ex d'attaques : buffer overflow, ROP ...
**Microarchitecture** : ce qui n'est pas connu du systeme (son fonctionnement)
👉️ Ex d'attaques : Spectre, zenbleed, rowhammer...
**physique** : le comportement physique
👉️ injection de faute
**Side channel** : Canal non prévu à la conception, qui permet de casser les algo de crypto par ailleurs safe.
Ex: consommation énergétique, champ elecmag, temps d'accès aux caches ... (ça n'était pas souhaité que ça donne de l'info)
## Attaques sur les caches
Principe de base : temps d'accès très différent selon la localisation de la donnée (cache L1, mémoire...).
Cache hit : la donnée est en cache => on l'a vite
Cache miss : la donnée n'est pas en cache => on l'a lentement
### Flush + Reload

--> besoin d'une bibliothèque partagée avec la victime
Fonctionnement :
- L'attaquant choisit une information
- L'attaquant `clflush` l'information (la renvoie en RAM) et attend
- La victime accède ou non à l'information
- L'attaquant regarde s'il a un cache hit ou miss
### Prime and probe

--> pas besoin d'une bibliothèque partagée avec la victime
Fonctionnement :
- L'attaquant remplis un set de données
- La victime accède ou non à l'information (et si c'est le cas écrase celles de l'attaquant)
- L'attaquant récupère des informations sur les addresses accédées
#### Pourquoi AES est-il faible \o/
**Dans Mix-column** :
Optimisation de T tables (plutôt que de faire une multiplication matricielle on fait une addition de look-up table). Un peu comme subbyte.

Dans ce cas vu qu'on va connaître les addresses accédées on va pouvoir en déduire les $C_i$ (l'état interne d'AES.
:::info
Conclusion : ne jamais faire d'accès mémoire dont l'addresse dépend d'un secret (tableau par ex)
:::
### Contre-mesures
#### Page coloring
chaque partie du cache a un processus associé.

#### Oblivious RAM
Tranformer l'algo en rendant les accès mémoire indépendant du secret (randomizer les accès mémoire).
#### Track and mitigate
Retirer/patcher les point spécifiques où un accès est sensible.
### Limitations des attaques sur les caches
- l'accès à une valeur proche en mémoire risque de fausser
- pre-fetch : accès anticipé à une addresse suivante (qui peut contenir le secret sans qu'on l'utilise)
Autre side channel : regarder combien de temps dure telle execution (on peut en déduire la valeur du `d` d'un RSA) ==> Mais plus pratique de regarder la consommation énergétique
## Attaque sur la consommation (Power-based)
Principe : on capture la consommation énergétique sur la machine (physiquement) ou dans un compteur de l'OS.
Avantages :
- peu détectable
- beaucoup de possibilités (ex: casser AES)
- difficile à mitiger (issu du matériel)
Désavantage :
- il faut avoir accès à la conso
- composants complexes $\Rightarrow$ traitement complexe (et donc bruité)
🎯 Cible principale : objets connectés / IOT (notamment les cartes banquaires)
### Simple power analysis :
Méthode d'attaque qui examine les profils de consommation différents pour en déduire quelle fonction est appellée.
Ex : trouver l'exposant de RSA
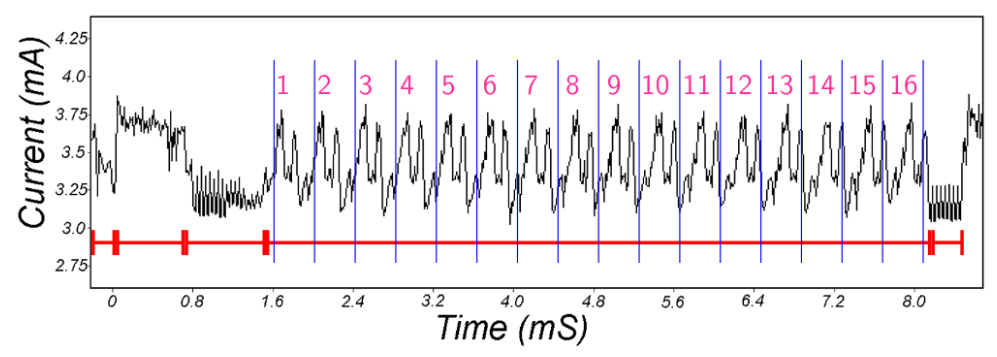
:::info
Tout algo dont le temps dépend du secret est attaquable. $\rightarrow$ ce qui dépend des secret doit être en temps constant.
:::
### Méthodes plus poussées
*Pourquoi ça marche ?*
Car $PT = C_{pd} × V_{CC}^2 × f_I × N_{SW}$
Tout est constant sauf le nombre de bitflips donc ça dépend du poids de hamming.
**Poids de hamming** : nombre de bits à 1 dans une variable (on s'abstrait de la position de la variable)
**Distance de Hamming** : nombre de différences de bits entre 2 variables (dans le cas actuel entre la variable avant et après)
Comment estimer la consommation à un cycle d'horloge :
On somme les distances de Hamming sur tous les registres.
$\large L(c_{j+1}) = \sum_i^n HD(R_i(c_j), R_i(c_{j+1}))$
Autres fuites : variation de vitesse de propagation : glitches.
Ex :
Si la seule chose qui change est `R1 = R1 & R0` avec R0 = (01001100) et R1 = (00111010) :
R0 & R1 = (01110110) ==> 5
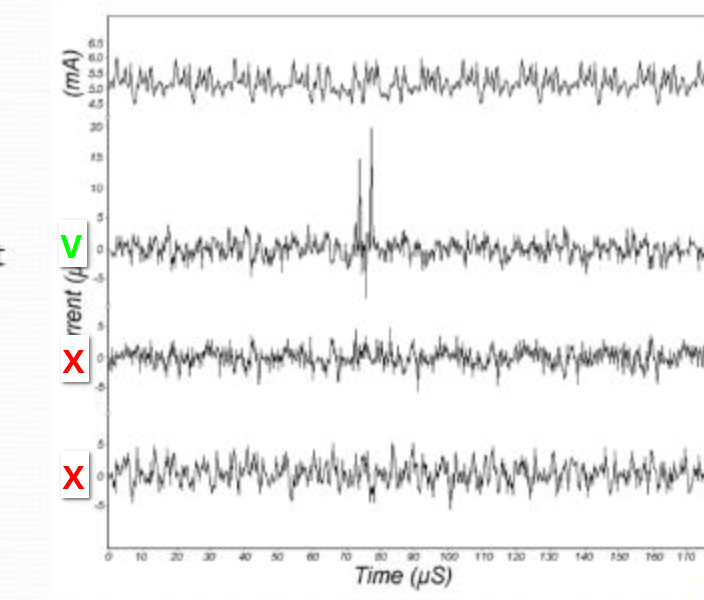
### Méthode Différentielle (DPA)
- on mesure beaucoup de traces de consommation
- On fait une hypothèse sur la clef et estimer la consommation (vu qu'on connaît la valeur résultante (le chiffré)).
- On trie les traces en 2 populations : une pour laquelle c'est élevé une pour laquelle c'est faible
- on fait une différence des moyennes et si c'est le cas il y a une forte différence au moment où la manipulation du secret a lieu
### Correlation Power Analysis (CPA) Attack
Utilisation d'un autre modèle du composant vierge pour faire un template et l'utiliser pour faire une comparaison de corrélation
$\a$ 10 fois moins de traces à obtenir par raport au DPA
### Comment se protéger?
techniques "bidouille" non prouvées :
- Réduire la consommation énergétique pour se rapprocher du bruit.
- calculer à la fois le calcul et son inverse pour avoir une consommation parfaitement constante
- désynchroniser pour que les comparaisons entre 2 traces ne marchent pas
- rajouter des calculs inutiles pour bruiter
Techniques prouvées de masquage :
Idée : mélanger les secrets à des valeurs aléatoires et uniformes
- Masquage booléen :
- $\begin{cases}
s_0 = s \oplus r\\
s_1 = r
\end{cases}$
- Masquage arithmétique :
- $\begin{cases}
s_0 = s + r\\
s_1 = r
\end{cases}$
Exemple : faire le \oplus de $m$ et $k$ :
$m$ => $(r1, r1 \oplus m)$
$k$ => $(r2, r2 \oplus k)$
$C1$ = $r1 \oplus r2$
$C2$ = $(r1 \oplus m)) \oplus (r2 \oplus k)$
C_final = $C1 \oplus C2$
= $r1 \oplus r2 \oplus (r1 \oplus m) \oplus (r2 \oplus k)$
= $m \oplus k$
::: info
on enleve le masque que sur une donnée qui peut être publique
:::