# Preuves formelles *À quoi que ça sert ?* À prouver (certification) la sécurité d'un système. - Pramatique : Qui parle de quoi : relation entre le langages et les utilisateurs - Sémantique : Abstraction du language, se réfère au sens de ce que l'on dit/écrit - Syntaxique : Abstraction du sens, se réfère à la formalisation de ce que l'on dit/écrit (ensemble des mots) Model d'un objet : abstraction qu’on observe sur un objet réel. Nécessite un language formel souple mais non ambigu. > M est un modèle d'un objet s'il permet à un observateur d'avoir des réponses à des questions qui l'intéressent. Un modèle est forcément incomplet, imparfait et fait des abstractions. ### comment qu'on bidouille les formules?    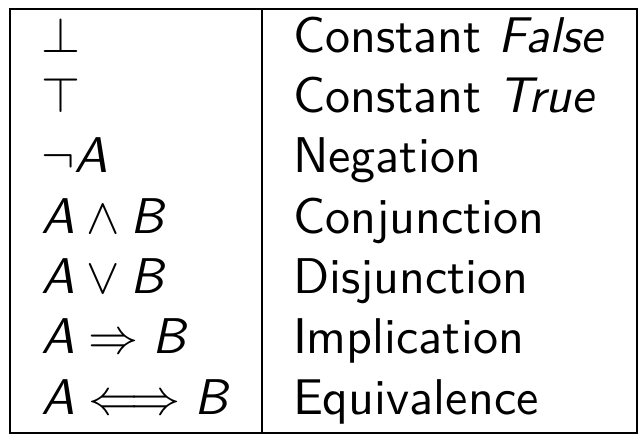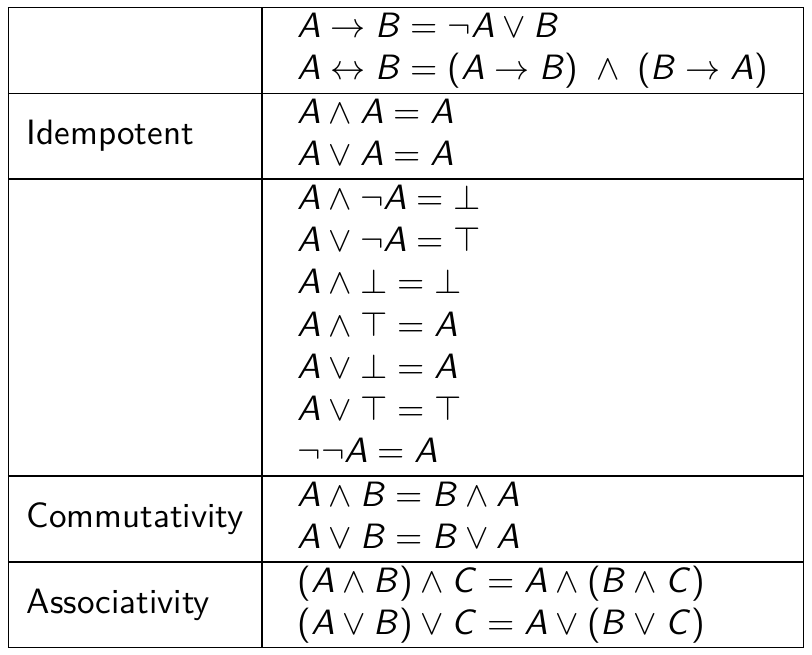### comment qu'on prouve les trucs?     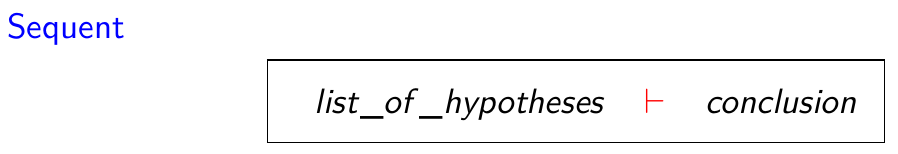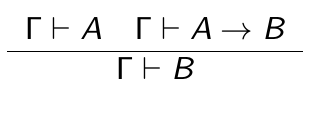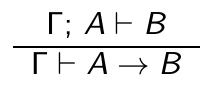- Le Et est non interférent (si on a démontré A et B on a A par ex) - Le Ou c'est l'inverse (si on a démontré A on a A Ou B par ex) Slide 21 : (flemme de retapper ça en latex), pour prouver on part de bas en haut mais la preuve se lit de haut en bas  Automatisation et tactique : La preuve sur la logique des propositions est décidable (Il existe un algorithme qui termine à tous les coups et résoud le problème). 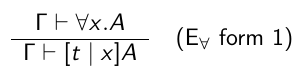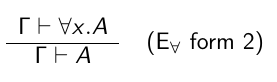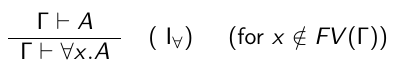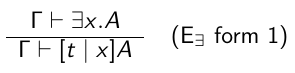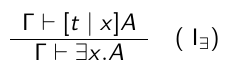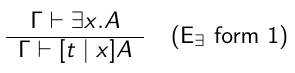Par contre la logique des proposition est très limitée (booléenne et pas numérique) Avec les $\forall$ faut mettre des implications, avec les $\exists$ il faut mettre un et ***j'ai pas compris pourquoi si quelqu'un peut aider ???***     [t|x] = remplace toute les occurrences de x par t preuve par témoin (si je veux démontrer qu'il existe un x ben j'en trouve un)   Dans la réalité on est pas si maso que ça donc on rajoute des trucs un peu plus vivables. Égalité : $A = B$ si tout prédicat vrai sur A est vrai sur B et équivalent --> on peut ensuite remplacer A par B (et inversement) Logique complète -> on peut tout démontrer Logique cohérente -> on ne peut pas se contredire dans nos preuves ### Théorie des ensembles *"On va tous galérer ça va être super"* Logique des ensemble : - rajoute le $E \in S$ - $E$ est une expression, $S$ un ensemble arbitrairement compliqué - Pour contreuire des ensembles, on peut : - lister $S := {1,2,3}$ - produit cartésien $S \times E := {(1 \mapsto a), (1 \mapsto b) \dots (2 \mapsto a) \dots}$ : ensemble de toutes les paires possibles - Le maplet ($\mapsto$) permet de ne pas faire de confusion dans la notation $(.,.)$ qui as plusieurs significations - ensemble des parties : ensemble de tous les sous-ensembles d'un ensemble - ensemble en compréhension : dire comment on peut construire la liste : $S := {x | P(x)} $ - Inclusion (relation d'ordre partielle): 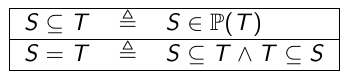 - opérations 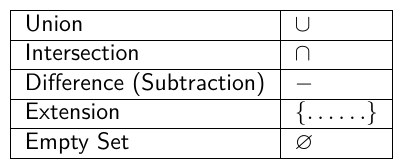 - souvent étudié avec un diagramme de Venn "Oulla non on va pas parler de ça" On peut définir une relation de S à T :  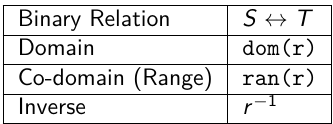Un ensemble de paire = Une relation entre 2 sets  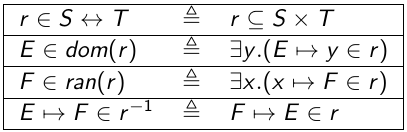Relation : - Partielle : implique pas tous les élément du domaine (dom\(r) != S) - Total : implique tous les élément du domaine (dom\(r) = S) - surjective si map tout les élément de l'image (codomaine)  Restriction de dommaines : on prend la même relation mais je garde dans la relation que ce qui concerne les éléments de f. 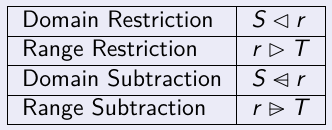On a des notations pour restreindre le domain/codomain :  Restriction ~ intersection, on chosi les éléments qu'on garde Substraction ~ "privé de", on choisi ceux qu'on dégage - Image relationnelle *Très utile* (en logique relationnelle) : ***Todo a compléter pas pu noter*** - Composition : relation telle qu'il existe des chemins entre le 1er et 3e ensemble - Composition : relation telle qu'il existe des chemins entre le 1er et 3e ensemble - $q \circ p = p; q$ (ie, ce n'est pas la loi rond, c'est un pipe !!)  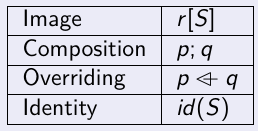Direct Product il a skip, first et second projection c'est pour ne garder que la première/seconde composante d'un couple (cf produit carthésien)  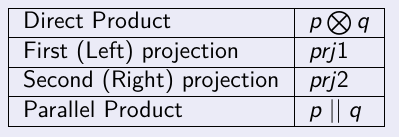Fonction = relation tq chaque élément de S ne map que vers un élément de T (c'est comme les applications en maths)  Encore des flèches, toujours plus de flèches, admirez ces flèchessssssssssss  (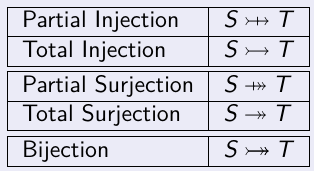parenthèse qui n'a rien à voir : isomorphisme : bijection qui préserve des bonnes propriétés et permet de passer d'un monde à un autre monde.) ### Définition de fonction - Liste de paire - compréhension  - $\lambda$ permet de faire des fonctions mais j'ai pas compris pourquoi Bonne définiton : $f(x)$ : on peu écrire ça si - f est une fonction - et $x \in dom(f)$. Si l'une des 2 propriété est pas vraie on a une bonne syntaxe mais une mauvaise sémantique. (exemple : erreur de typage) Il en a parlé de ça ? (non)  Le prof dit d'aller voir le problème du castor affairé et ça a l'air assez marrant. *J'ai pas compris ce qui suit si quelqu'un veut m'éclairer* Je crois qu'un modèle peut être vu comme un automate, d'om les états & co, avec chaque variable qui est valuée (par ex. x = 3, x n'est pas non-défini)   (Ici y'a une typo, et BAA c'est en français, c'est BAP en anglais) Aussi la simultanéité n'existe pas (le temps est "trop précis" pour qu'il y ait une simultanéité parfaite) $\tau$-transition : globalement c'est un changement qui fait rien mais dont on s'en fout, typiquement quand on fait du python il peut y avoir des flags qui change sur notre CPU bah on s'en fout royalement ### Sûreté = éviter les "trucs dangereux" : assurer une propriété (la sûreté c'est pas une propriété mais je sais plus ce que c'est lol) qui doit être vrai à tout moment (ex : à tout moment on se crache pas ?????) : invariant Invariant : Propriété vraie sur tous les états Prouver la sûreté c'est compliqué parce que y'a pleins d'états, c'est pas déterministe etc. ==> Mais on peut procédér par induction (on connaît les variables et événements mais pas les états (POURQUOI???)). : - Du coup on va partir d'un état de base sûr - Et on va vérifier que tous les états atteignables par induction. - Pour que ça marche nos états sont des états d'invariants (si quelqu'un a compris pourquoi je suis preneur !) ### Vivacité (bisous Mr vernandat) - on veut que tel état soit accessible - Variant (kécécé?) Ex : une suite d'entier positifs décroissant atteint 0 (je suis pas sûr d'avoir compris ça) ## EVENT B - Apparemment c'est super important - ça sert à représenter des systèmes avec un état concret - basé sur la logique du premier ordre. - Utilie pour les SC et pour ce qui est basé sur des événements (donc tout?) - système de modèles permettant de démontrer des trucs grâce à un modèle correct par construction Mécanisme de rafinement : - je pars d'une spec abstraite - je fais de la magie (c'est vraiment ce qu'il a dit le prof) pour rajouter des détails - si j'ai bien ratjouté des détails mon modèle reste correct mais + précis - À la fin on a du B0 et ça génère du code correct par construction C'est la seule méthode du monde qui fait ça et c'est vraiment trop bien ouahou houahou 🙌🏼 Liste des trucs sur un Event-B: - machine - Context - Extends - Sets - Constants - Axioms - Theorems - End Risque des Axiomes : - ils peuvent être contradictoires - ils peuvent avoir des axiomes qui admettent pas d'évaluation Machine / Refines / sees / Variables / Invariants / Theorems / Variant / Events / End Parmis la liste des évents on a l'initialisation. Les variables ont toutes une valeur (elles ne peuvent pas ne pas être initialisée). Evenement définit par quelque chose entraine une action :| c'est un smiley modérément content De la syntaxe pour manipuler les variables dans Event-B :  Exemple de ce qu'on peut faire  Garde : Permet de filtrer suivant un évement particulier (un peu comme un if) ANY . : On en a besoin, on sait qu'on l'aura d'une façon ou d'une autre mais osef du comment donc on le traite comme un truc qui est entrant à un moment mais on sait pas pourquoi ni comment Obligation de preuve : un séquent qui permet de vérifier qu'on a un truc qui marche suivant certaines contraintes ??? (si quelqu'un a compris please rajoutez infos)   digression du prof : les action n'ont jamais lieu en même temps mais elle peuvent être atomique et là elles sont pas en même temps mais un peu quand même je crois Je crois que ce qu'il voulait dire c'est que les actions après un THEN sont atomiques. Une action atomique on peut la traiter comme 1 seule opération, tout sera effectué et le système ne pourra rien faire entre les opérations de l'action atomique, avec la subtilité ici que les lignes peuvent être vuent dans n'importe quel sens (x = a puis y = b c'est pareil que y = b puis x = a). 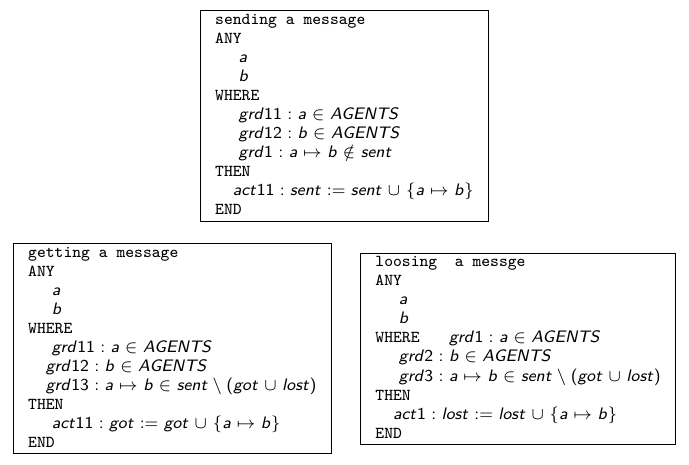### Exemple de système modéliser, l'envoi de de données entre agents: Un agent ça peut être un peu n'importe quoi (processus, serveur, une personne...)    Infos en vrac incomprises : - on n'a accès qu'à des entiers et de booléens - on fait du rafinement où on change les variables en précisant les événements mais j'ai pas compris ce que c'est. Ça permet de rendre des gardes plus fortes (donc par exemple faux et ça j'ai vraiment pas compris !?????) - on a des invariants de collage qui sont vrai des 2 côtés d'un carré (et c'est une forme de rafinement je crois) - différence événement concret et abstrait : - skip c'est le truc qui fait rien et change $x$ en $x$ et on peut le rafiner pour ?????? : - on peut faire $G(x) \Rightarrow \top$ et on a $G(x) \land BAP(x,x')$. J'ai rien compris ??? - Paramètre d'événement : heu ça existe et on peut les fixer mais j'ai pas compris à quio ça sert : représente une valeur qui apparaît quand j'en ai besoin puis plus tard on dit comment elle apparaît avec BOARD et SIN (je sais pas ce que c'est) - on peut générer par du code des rafinement qui génèrent un modèle qui génère du code. J'ai laissé tomber de comprends/noter au moment de l'exemple de la vente en ligne