# TP Event-B Notes \*magnifiques\* de Karine : https://docs.google.com/document/d/1yzV2_qVrvchvByIVfPt6NzjZrhwETJrAF8wPDtQQESM/edit?usp=sharing  :::danger La rédaction de ce TP tient à exprimer ses excuses par avance concernant la non-fiabilité des réponses (et des questions d'ailleurs...) ::: # I Abstraction ## Question 1 > Devra-t-on modéliser chaque type d’automate que l’on voudra implémenter ? Est-il pertinent de modéliser (à ce niveau) le mode de transport des cartons ? Le contenu des cartons ? Les cartons ? Dressez alors une liste exhaustive et minimale de ce dont on a besoin pour écrire ce modèle abstrait. Donnez ensuite les opérations les plus basiques dont devrait être capable le système. - Non non et non - Notions à définir : - objet/carton - point - déplacement : - attente - en cours - arrivé - ensembles de cartons à déplacer, deplacés et perdus Propriétés : 1. L’automate ne perd pas de carton 2. L’automate finit par traiter tous les cartons ## Question 2 > Exprimez la propriété (1) avec la logique d’Event-B (premier ordre et théorie des ensembles). De quel genre de propriété s’agit-il ? Types d'exigences: * Exigence fonctionnelle := "ce que le système doit faire" * Exigence de sûreté := "ce que le système ne doit pas faire / doit garantir" * Convergence (ou terminaison) := "le système atteint une fin" :::warning 1ère idée : ```#(cartons en entrée) = #(cartons en sortie)``` $\Rightarrow$ Faux car si on recoit 10 cartons en entrée et 10 cartons en sortie, rien ne garanti que ce sont les même (correction du prof) ::: :::success Corrections (les 3 sont éauivalents) : - en français : Un carton est soit en entrée soit en sortie - $\forall c, c \in Entrée \lor c \in Sortie$ - $\rightarrow$ on considère que pour l'instant il ne peut pas être en transit - $cartons = Entrée \cup Sortie$ et $Entrée \cap Sortie = \emptyset$ - Avec `cartons` l'ensemble des cartons qui nous intéressent (alors que `CARTON` est l'ensemble de tous les cartons) ::: Je demande au prof <3 :heart: Ok du coup $Entrée \cap Sortie = \emptyset$ c'est inv3 mais du coup la propriété de la quesiton 1 il fallait l'avoir si on voulait que ça fasse totalement sens je crois ok merci trop bien les profs qui se contredisent zzZzz :sleeping: # II Modèle Event-B  ## Question 3 > 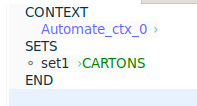Écrivez l’invariant auquel cela correspond (inv3 $\rightarrow$ inv4 ici parce que Estelle préfère mettre les invariants qui se ressemblent ensemble). ``` MACHINE Automate_0 › SEES ⚬ Automate_ctx_0 VARIABLES ⚬ Cartons › ⚬ Entrée › ⚬ Sortie › INVARIANTS ⚬ inv1: Entrée ⊆ CARTONS not theorem › ⚬ inv2: Sortie ⊆ CARTONS not theorem › ⚬ inv3: Cartons ⊆ CARTONS not theorem › ⚬ inv4: Entrée ∩ Sortie = ∅ not theorem › ⚬ inv5: Entrée ∪ Sorties = Cartons not theorem › EVENTS END END ``` :::success L'invariant à rajouter est donc `inv4: Entrée ∩ Sortie = ∅ not theorem ›` ::: ## Question 4 > Que contiennent les ensembles Entrée et Sortie au tout début du fonctionnement de la machine ? Déduisez-en les actions à écrire dans l’événement INITIALISATION. ``` INITIALISATION: ⚬ Entrée := CARTONS; ⚬ Sortie := ∅; ``` ## Question 5 > Où l’automate peut-il prendre un carton ? Déduisez-en la garde grd2 de l’événement Prendre. ``` ⚬ PRENDRE: not extended ordinary › ANY ⚬ c › WHERE ⚬ grd1: c ∈ Cartons not theorem › ⚬ grd2: c ∈ Entrée not theorem › ⚬ grd3: c ∉ Sortie not theorem › END ``` ## Question 6 > À quelle(s) condition(s) un carton peut-il être déposé sur la sortie ? Déduisez-en la garde grd2 de l’événement Poser. (On prendra soin de ne pas déposer un carton qui est déjà sur la sortie, ni un carton qui n’a pas encore été pris par l’automate.) ``` ⚬ POSER: not extended ordinary › ANY ⚬ c › WHERE ⚬ grd1: c ∈ Cartons not theorem › ⚬ grd2: c ∉ Entrée not theorem › ⚬ grd3: c ∉ Sortie not theorem › END ``` ## Question 7 > Comment écrire le fait de retirer ou d’ajouter un carton à l’entrée et à la sortie ? Déduisez-en les actions à écrire pour Prendre et Poser. (Attention à bien identifier ce qui est un ensemble et ce qui est un élément de cet ensemble.) ``` POSER act1: Entrée := Entrée \ {c} PRENDRE act1: Sortie := Sortie U {c} ``` ## Question 8 : > Les affectations faites dans l’événement INITIALISATION respectent-elles bien tous les invariants ? Oui. ## Question 9 : > Qu’est-ce qui garantit que des opérations telles que \ (différence ensembliste) et ∪(union ensembliste) ne changent pas la nature des ensembles utilisés dans le modèle ? (Autrement dit que les ensembles restent des ensembles de cartons.) Parce que c'est des éléments du même type ??? ## Question 10 : > Donnez un argument (informel) au fait que des cartons ne se dupliquent pas. Est-il possible que des cartons disparaissent ? L'invariant 4 (l'invariant 3 du sujet). 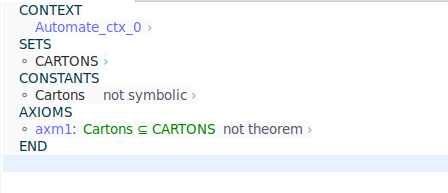### Version avec petits Cartons Cartons est un sous-ensemble de CARTONS, il représente les cartons qui nous intéressent à déplacer  - ajout pour simulation : axm2 : card(Cartons) = 2;  # II Raffinement ## Question 11 : > Quel est le type de Transit ? Quels invariants, similaires à l’invariant inv3 de la première machine, permettent de signifier qu’un carton ne peux pas être à la fois en entrée, en transit et en sortie ? - Ensemble de carton (`Transit ⊆ Cartons`) - ``` Entrée ∩ Sortie = ∅ Transit ∩ Sortie = ∅ Transit ∩ Entrée = ∅ ``` ## Question 12 : > Exprimez sous la forme d’un invariant le fait qu’un carton est toujours en entrée, en transit ou en sortie. ``` Entrée ∪ Transit ∪ Sorties = Cartons ``` ## Question 13 : > Exprimez sous la forme d’un invariant la propriété suivante : « S’il n’y a pas de carton en entrée ou en transit, alors la sortie contient tous les cartons. » ``` Entrée = ∅ ∧ Transit = ∅ ⇒ Sortie = CARTONS ``` :::info C'est un théorême, dans le cas présent apparement ça permet de vérifier que les règles au dessus collent bien à ce qu'on veut faire (si ça colle pas on aurait une erreur). À peu près aussi utile qu'un cours de SHS quoi. ::: ## Question 14 : > Que contient la variable Transit à l’initialisation ? Déduisez-en l’initialisation de cette variable dans l’événement INITIALISATION. ``` Transit = ∅ ``` ## Question 15 : > Comment évolue Transit lorsque l’on prend un carton de l’entrée ? En déduire la ou les actions à ajouter à l’événement Prendre. Doit-on modifier les gardes de l’événement ? ``` act1: Transit := Transit U {c} ``` ## Question 16 : > Comment évolue Transit lorsque l’on pose un carton de la sortie ? En déduire la ou les actions à ajouter à l’événement Poser. Doit-on modifier les gardes de l’événement ? ``` act1: Transit := Transit \ {c} ``` ## Question 17 : > Déchargez les autres obligations de preuve de la première machine du mieux que vous pouvez. ``` act1: Transit := Transit \ {c} ``` ## Question 18 : > Déchargez les obligations de preuve de la deuxième machine. 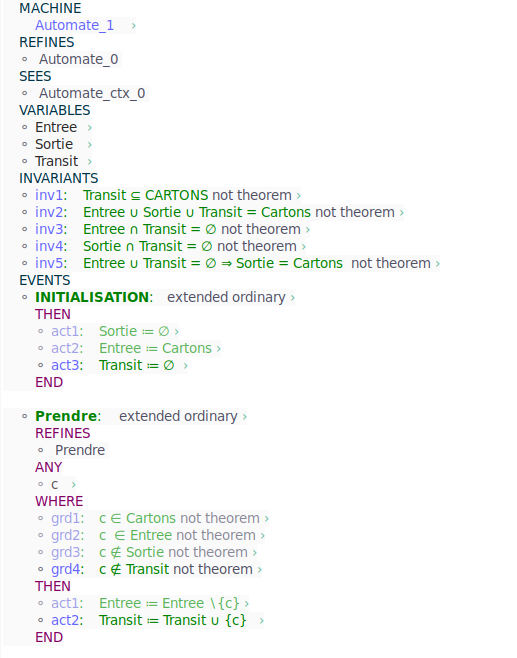``` act1: Transit := Transit \ {c} ``` ### Version avec petits Cartons   ## Question 19 G{Entrée ∪ Transit = ∅ } => F {Sorties = Cartons} ## Question 20 G{ Transit /= ∅ } => [Poser]