# Symmetric Encryption Chapitre précédent : [Théorie de l’information et Cryptographie](https://notes.ar-lacroix.fr/s/avg_gtXSt) ## Quelques chiffres **Substitution monoalphabétique: Chiffre de César** - Chiffre de César est pas inutilisable, mais est seulement utile pour des messages très petits - Limitations: L’analyse fréquentielle des symboles permet de les déterminer **Substitution polyalphabétique: Chiffre de Vigenère** - Paramétrer la translation en fonction d'une clef qu'on répète - Limitations: - N’empêche pas l’attaque fréquentielle, - En effet on peut répéter l’attaque pour des sous-ensemble de la clef (pour chaque caractère) **Chiffre de Hill** On multiplie le bigramme (2 chars) par une matrice. On déchiffre en multipliant par la matrice inverse. Pour un matrice de taille 2 on a $2^{17.26}$ clefs différentes D'ordinaire on recommande 2^80, l’exposant (80) correspond au niveau de sécurité 2^N indique le nombre d’opérations qu’il faut pour casser un algorithme de chiffrement ### Définitions **Distance d’unicité** Nombre minimal $d$ de chiffrés $C$ nécessaires à un attaquant pour pouvoir déduire la clef de déchiffrement $K$sans ambiguïté. Il faut que l’entropie de la clef, connaissant les $d$ chiffrés, soit nulle. Autrement dit: $$H(K|[C_1, C_2, C_3, ...]) = 0$$ **Entropie** Évalue le débit d’information, pour ça il faut savoir ce qu’est une quantité d’information Quantité d’information - Un évènement qui se produit, produit de l’information - Plus l’évènement est rare, plus il produit de l’information - D’où la quantité d’information d’un évènement = `-log2(P1[E])` - plus d’infos: [https://fr.wikipedia.org/wiki/Entropie_de_Shannon](https://fr.wikipedia.org/wiki/Entropie_de_Shannon) Au fur et à mesure qu’on aura des chiffrés on aura de plus en plus d’information sur la clef jusqu’à ce qu’on ait assez d’information pour la déduire sans ambiguité On peut calculer la valeur de $d$ grâce à la distance d’unicité.  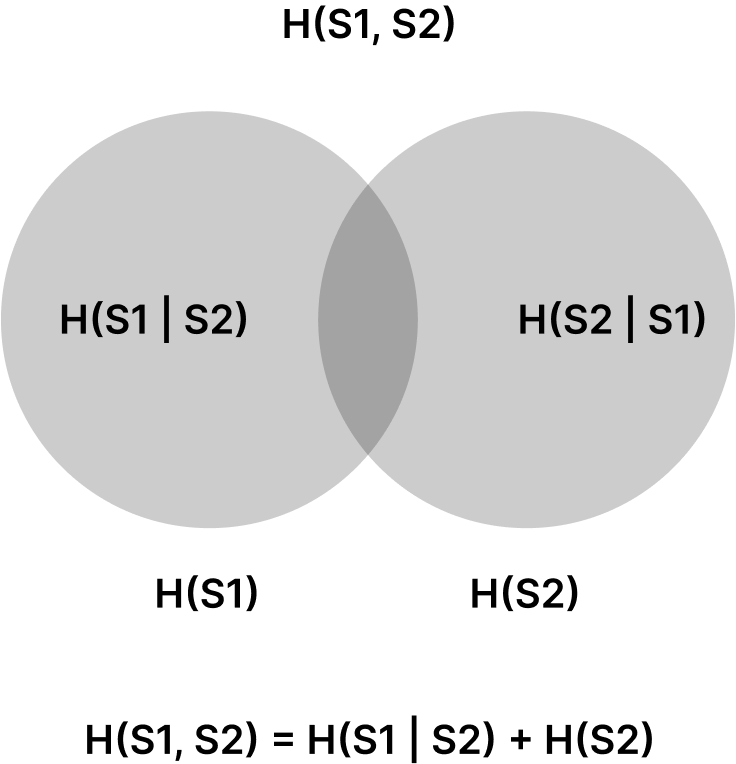$= H (K, C_1, ..., C_d) - H(C_1, ..., C_d)$ $= H(K, M_1, ..., M_d) - H(C_1, ..., C_d)$ $H(K) + H(M_1, ..., M_d) - H(C_1, ..., C_d) = 0$ On passe de la première à la deuxième en se disant que connaitre d chiffrés et la clef c’est comme connaitre les d clairs et la clef (car on a un chiffrement symétrique) ### Application: Substitution Mono-Alphabétique - $H(K) = 26!$ Pour A j’ai 26 chiffrés possibles, puis B je n’ai plus que 25 chiffrés possibles, puis C plus que 24, etc. Pour calculer l’entropie: $log_2$ du nombre de possibilités de clef : $$ H(K) = \sum{p(k_i)\times log_2(\frac{1}{p(k_i)})}\\ = \frac{26!}{26!}log_2(26!)\\ = log_2(26!) $$ Pour calculer l’entropie de la source, on choisit une clef on chiffre tout le texte, puis on refait la même chose avec des clefs différentes et on concatène tous les chiffrés différents, et on calcule l’entropie de cette concaténation. $$ d = \frac{log_2(26!)}{4.34-3.94} \approx 188 $$ Au bout de 188 caractères émis avec la même clef, l’attaquant peut être *certain* d’avoir la clef (mais pas besoin de 188 caractères pour décoder, seulement pour que la probabilité d’avoir la clef soit de 1) <aside> ⚠️ Cette valeur est uniquement valable pour le texte dont l’entropie a été calculée </aside> [https://www.bibmath.net/crypto/index.php?action=affiche&quoi=complements/imperfection](https://www.bibmath.net/crypto/index.php?action=affiche&quoi=complements/imperfection) **Chiffrement par transposition** Changement de l'ordre des charactères Exemple : croix greque, problème : la clef de sécurité est la manière d'agencer --> mauvaise pratique la clef doit être séparée de l'algo de chiffrement ### Cryptographie Moderne : On mélange substitution et transposition. **Les 2 principes de Kerckhoffs** - Le cryptosystème doit être, si il n’est pas théoriquement inviolable, inviolable en pratique --> niveau de sécurité - La conception d’un cryptosystème ne doit pas contenir de secret, et compromettre le cryptosystème ne doit pas amener l’effondrement de la sécurité --> Paramétrer une machine en fonction de la clef, au lieu de l’inclure dedans **Exemples : Chiffre ADFGVX** matrice de lettres puis transposition par rapport à un mot qui sert de clef.  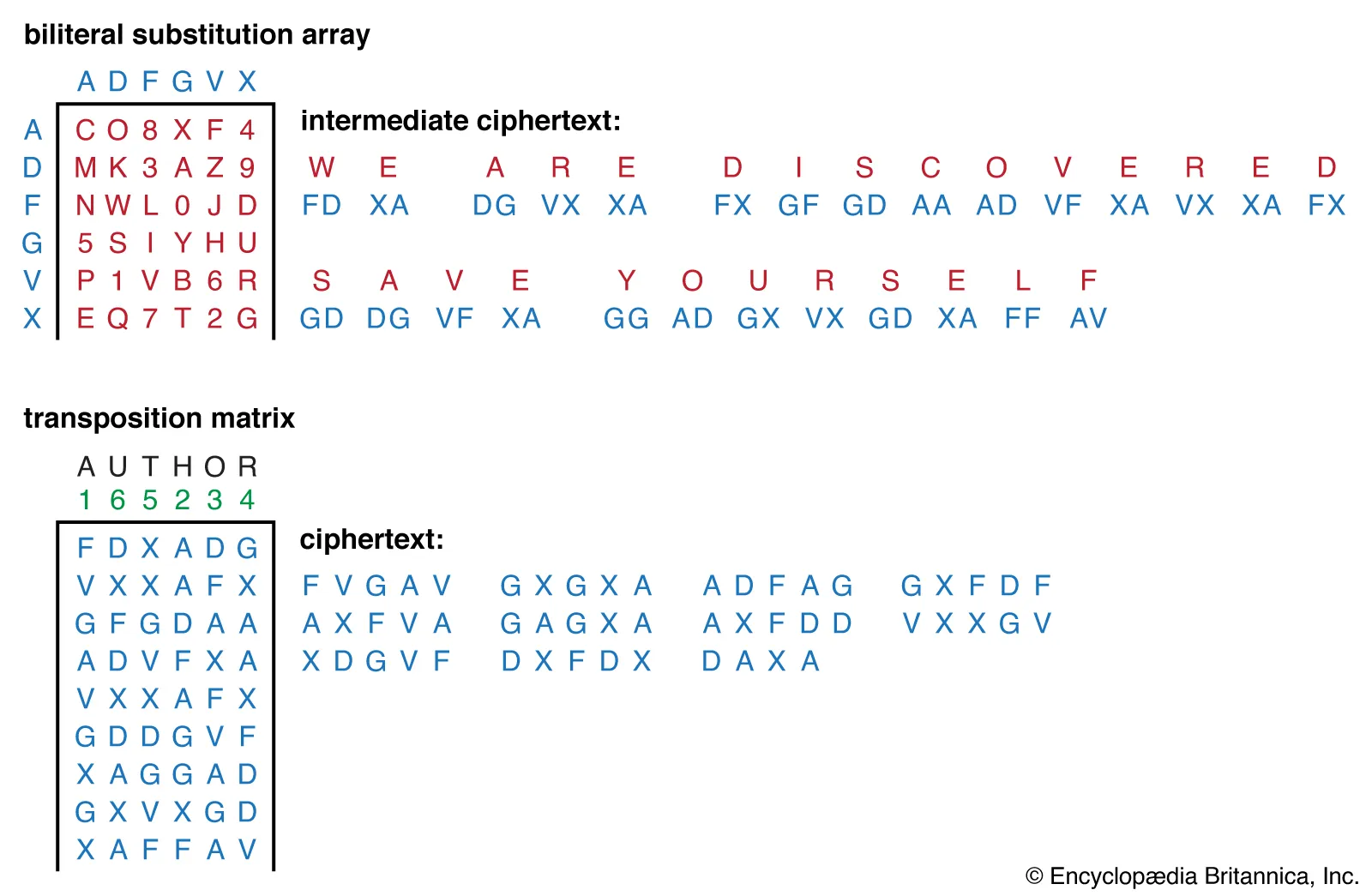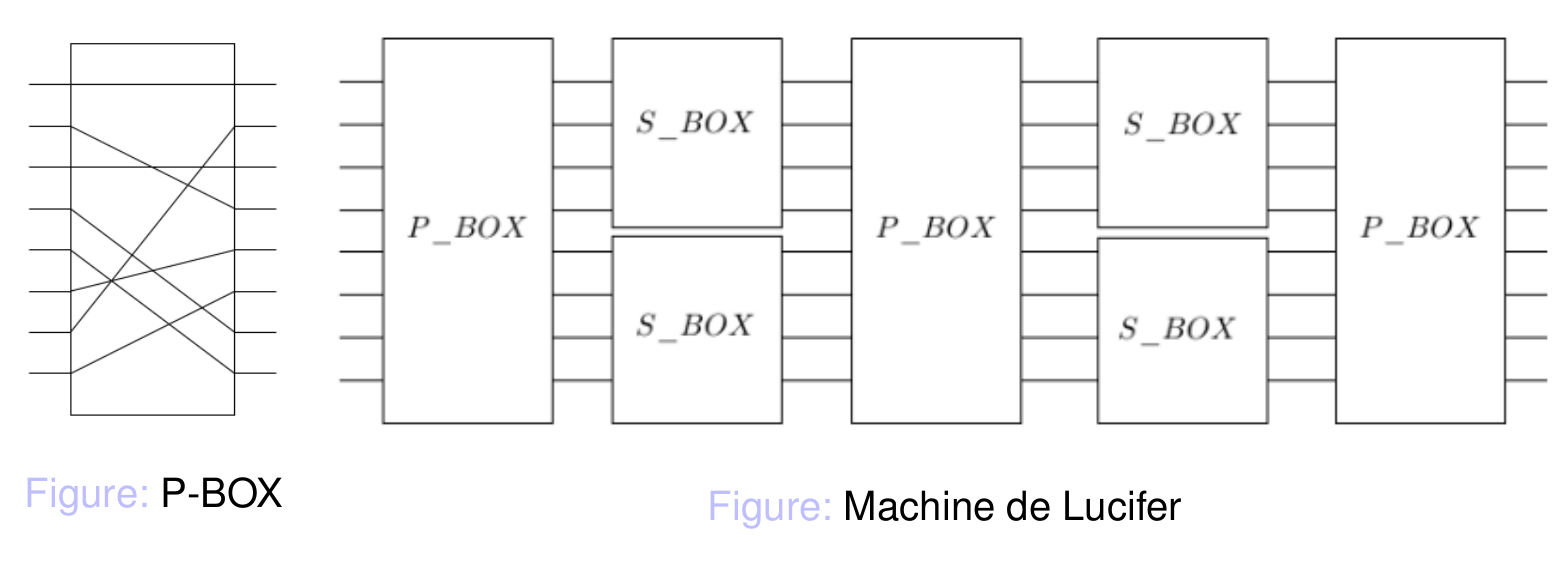**Exemples : Machine de lucifer** Chiffrement avec des blocs transposition et des blocs de substitution :  Shannon est revenu en scred avec 2 nouvelles propriétés - Diffusion: Si on change 1 bit du plaintext, au moins 50% des bits du ciphertext seront changés par rapport au ciphertext original --> Permet de protéger le clair - Confusion: 1 bit du chiffré doit être relié à plusieurs bits de la clef. on veut rendre la relation clef/chiffrée la moins utilisable possible --> Permet de protéger la clef --> non-linéarité de l'algorithme Pour une machine de Lucifer : - La S box casse la linéarité et crée donc de la confusion - L'ensemble d'une cascade de S et P crée de la diffusion ## **AES (Advanced Encryption Standard)** ### 2 Types de chiffrement **Chiffrement par blocs** - On découpe le message à chiffrer en bloc de taille $n$ - La clef est générée de façon aléatoire, de taille $k$ - Chaque bloc va être chiffré avec la même clef via un algorithme de chiffrement  - 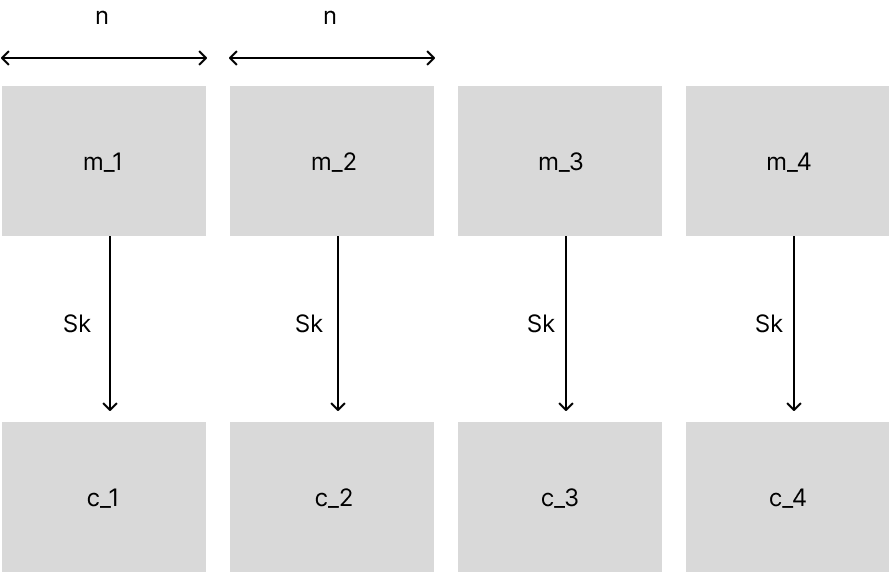Dans ce schéma si `c_1 = c_3` on peut alors déterminer que `m_1 = m_3` donc en réalité on va rajouter des mécanismes pour pallier à ça et qui fait (pas sûr que ce soit ça?) qu’on ne peut pas sélectionner et déchiffrer seulement un segment ou un bloc mais qu’on doit faire tout le message **Chiffrement à flot** - Algorithme “Keystream”: permet de générer une clef de grande taille (exemple ChaCha20) - Cet algorithme prend en entrée une clef de taille fixe - On va effectuer un XOR entre le clair et la clef précédemment générée - On va également avoir un algorithme pour vérifier l’intégrité du chiffré  - Utilisé en embarqué parce qu’on considère que l’embarqué envoie des tonnes de données, et le chiffrement à flot a comme propriété qu’on peut déterminer un segment de la clef sans avoir à partir du début, et ça permet au serveur de déchiffrer et récupérer uniquement les données qui l’intéressent sans avoir à tout déchiffrer et tout regarder **Construction d’un chiffrement par bloc** - Assomption: les algos de chiffrement par blocs sont sécurisés s’ils assurent randomness suffisante dans la permutation des ??? - Formally - Challenge ### Réseaux de Substitution et Permutation (SP Network) - Succession de substitution et permutation paramétrées avec une clef - Les S/P doivent être inversibles - Chaque itération est un “round” - Le plus d’itérations on a, le plus la diffusion et confusion sera importante - Trouver des informations sur le clair doit être aussi complexe que faire une recherche exhaustive (bruteforce) sur la clef (niveau de sécurité à peu près égal à la longueur de la clef) Si le réseau SP est bien foutu, retrouver la clef revient à faire une recherche exhaustive (bruteforce) **Deux approches** - S/P pseudo-random et clef unique - S/P fixe et clef pseudo-random - La plus simple à implémenter c’est la fonction de S/P unique, et générer une clef aléatoirement Substitution (S-Box) → Remplacer un symbole avec un autre - Créer de la confusion (rend la sortie non-intelligible) - Contribue à la non-linéarité $\iff SBox(v_1 \oplus v_2) \neq SBox(v_1) \oplus SBox(v_2)$ Permutation (P-Box ou D-Box) → Échanger la place deux symboles - Créer de la diffusion (les bits seront répartis partout dans l’état interne) - C’est linéaire, d’où le besoin pour la substitution $PBox(v_1 \oplus v_2) = PBox(v_1) \oplus PBox(v_2)$ Importance de la non-linéarité: $\Delta Y = PBox(PBox(X_1\oplus\ X_2))$ ### Construction d'AES - on découpe le clair en blocs de 16 Octets - on chiffre par bloc avec des réseaux SP  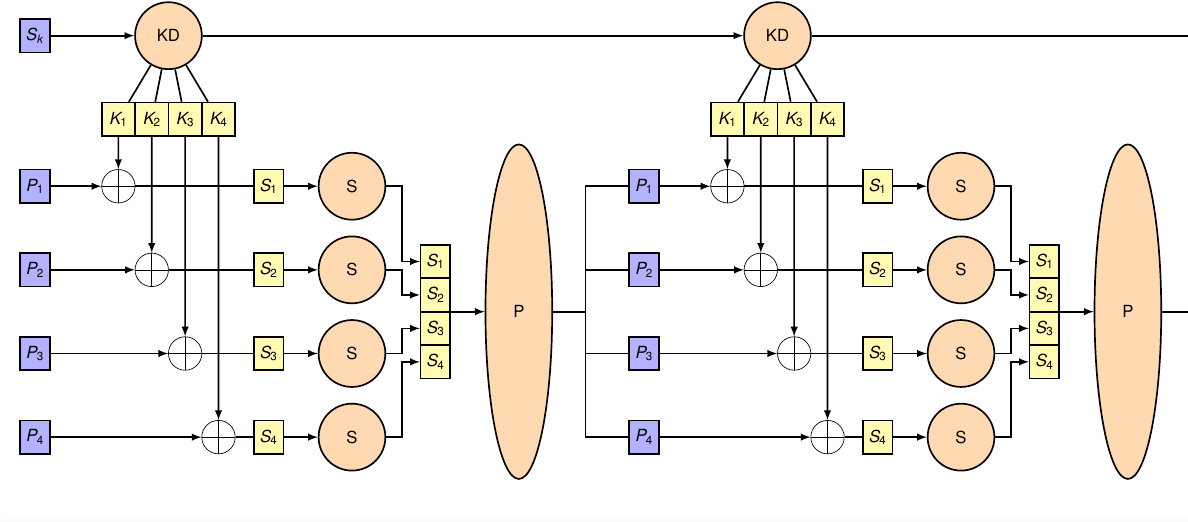2 tours de AES, le nombre de tours dépend de la taille de la clef car au bout d'un moment sinon on aura épuisé l'entropie. 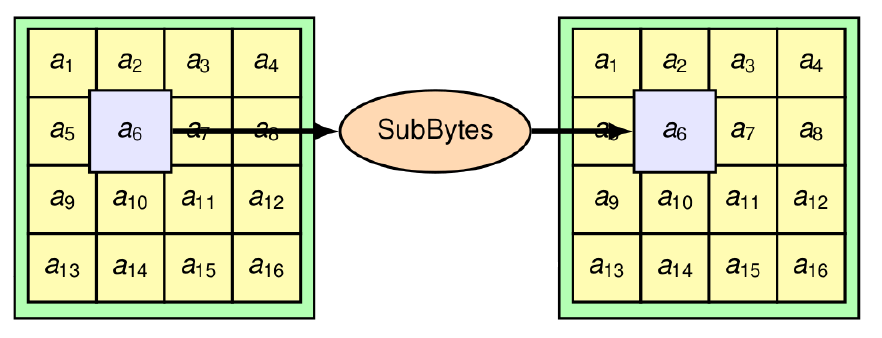**[Une super animation qui explique la base de AES très visuellement](https://formaestudio.com/rijndaelinspector/archivos/Rijndael_Animation_v4_eng-html5.html)** 3 phases principales dans son réseau SP:  **SubBytes (Substitution)** - Substitution d'un octet par un autre - Non-linéarité - Complexité: Expression complexe dans un champ de gallois ($GF(2^8)$) - Implémentation simple: Lookup table nécessaire On applique 2 transformations successives : --> inverse -- opération de transformation affine : $b(x) = (x^6+x^5++x+1)+a(x)(x^7+x^6+x^5+x^4+1) \; mod (x^8 + 1)$ G = Corps de Gallois On représente notre séquence de bits comme étant un polynome qui a 8 coefficients, on construit un corps derrière avec des additions et multiplications polynomiales (modulo un polynôme irréductible) L’addition de deux polynôme dans GF(2^8) (sachant que les 2 polynômes sont dans Z 2) c’est faire un XOR  **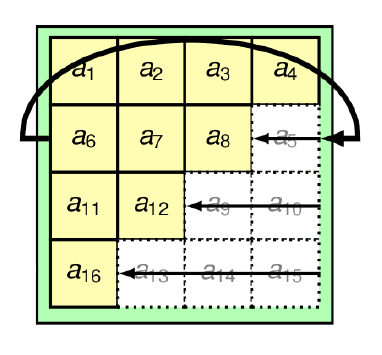ShiftRows (Permutation 1)** - transposition sur les lignes : rotation de 8 bit à gauche (1 octet)  **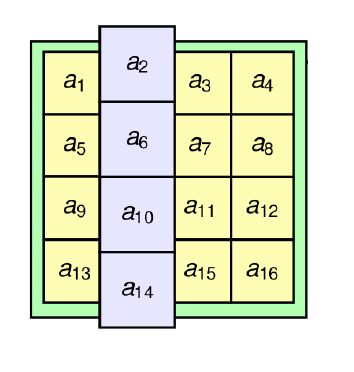MixColumns (Permutation 2)** - On va mélanger les coefficients colonne par colonne, ce qui est équivalent à multiplier chaque colonne par la matrice suivante: ?  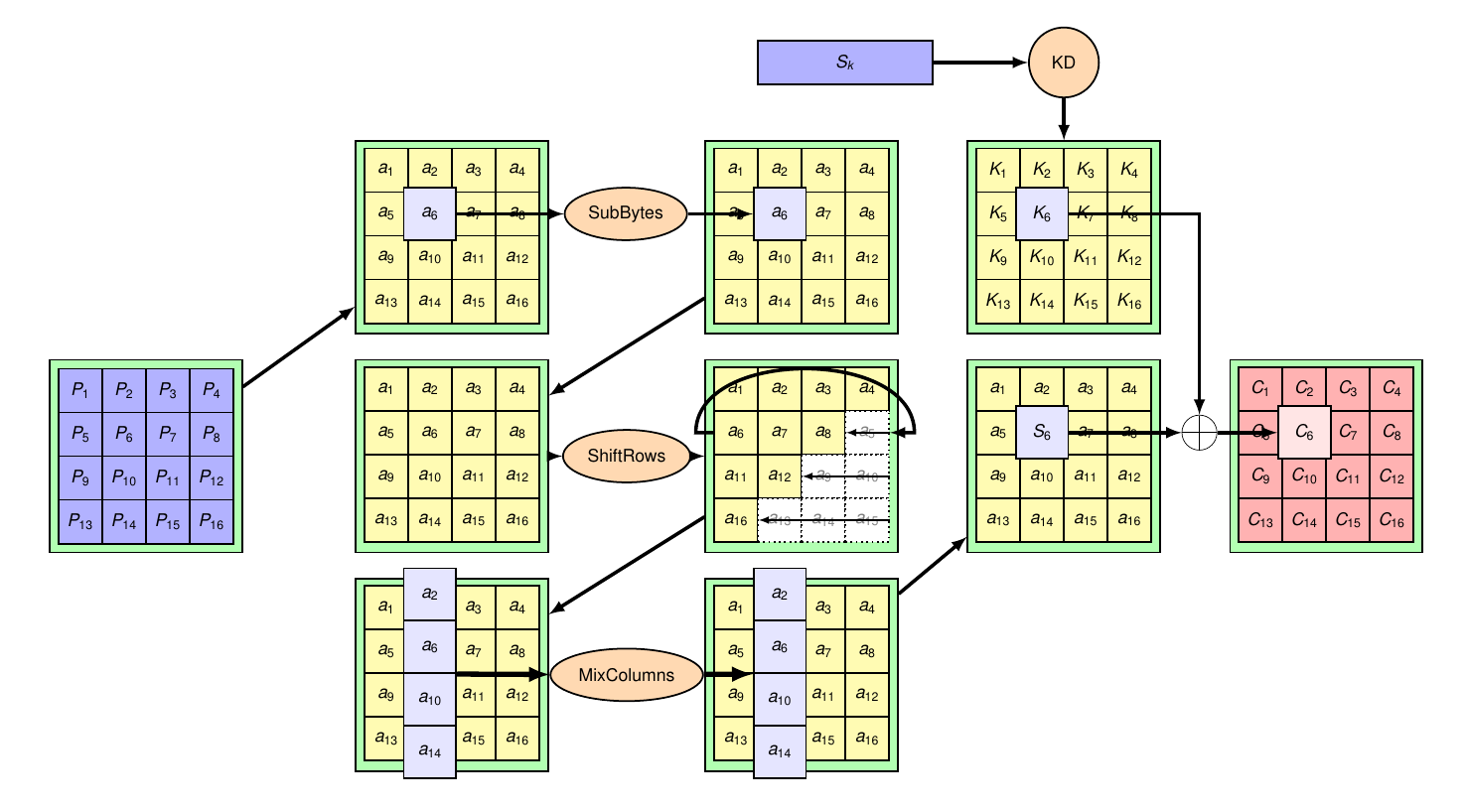[https://www.utc.fr/~wschon/sr06/txPHP/aes/MixColumn/MixColumn.php](https://www.utc.fr/~wschon/sr06/txPHP/aes/MixColumn/MixColumn.php) **AddRoundKey** On XOR avant chaque round : Chiffrement: $\oplus \implies SBox \implies PBox \implies \oplus \implies SBox \implies ...$ ==> Très optimisé (qq cycles pour une éxécution) ### récap AES  ## Évaluation de la sécurité La meilleure attaque connue sur AES est la recherche exhaustive. Une méthode permet de retirer 2 bit de sécu au nombre de bits de la clef donc taille de clef $\approx$ niveau de sécu.  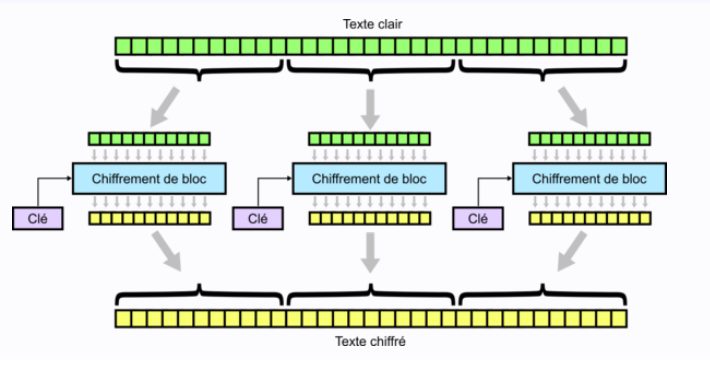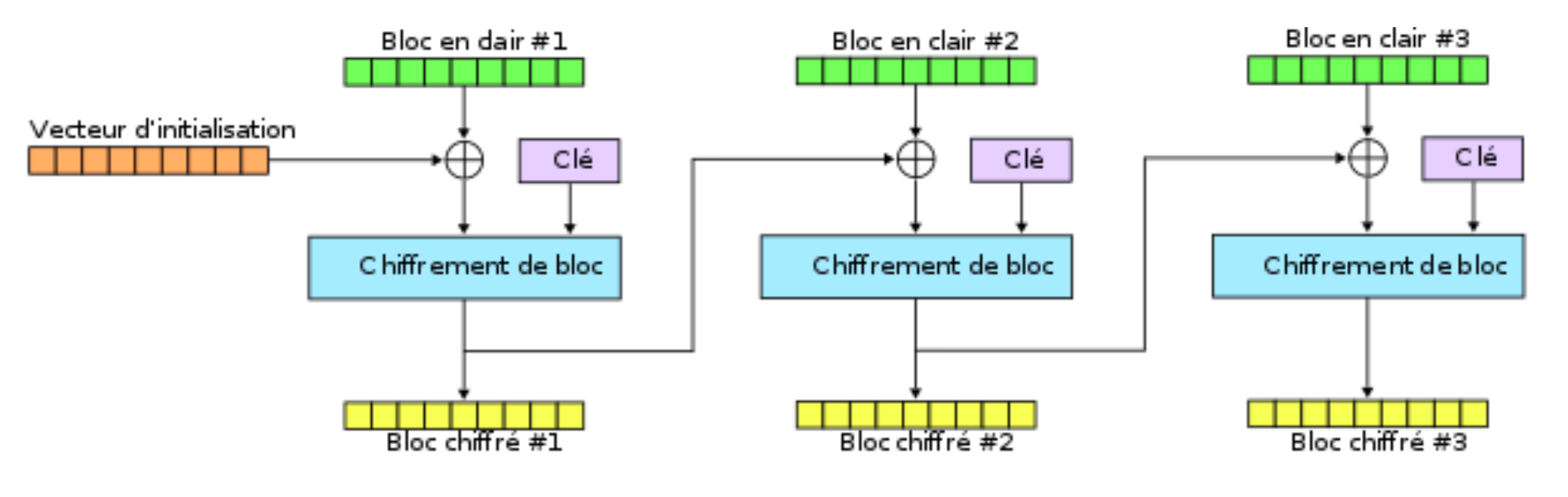<!-- 🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧 Fin des Fiches Anki 🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧 --> ### Différents modes d'AES --- Mode d'opération ECB **(PAS BON !)**  Mode d’opération CBC: **(POTENTIELLEMENT PAS BON !)**  --> mauvais si le VI est constant ou prédictible mais bon sinon. 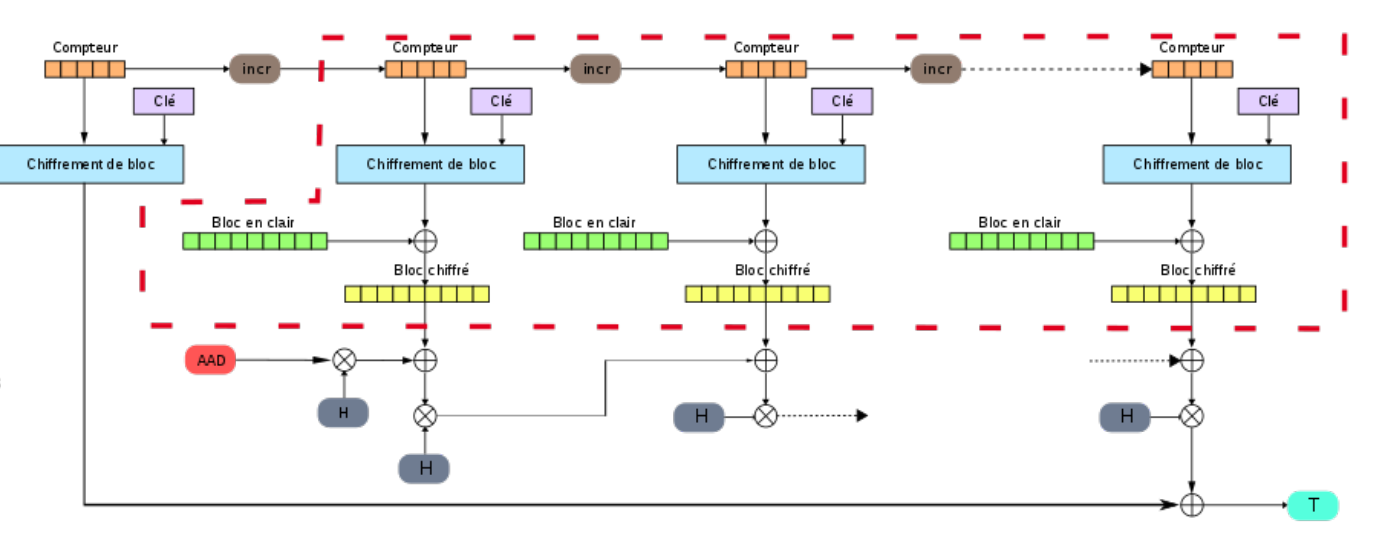Mode d’opération GCM: **BON !**  On génère un compteur chiffré en bloc qui est XORé avec le clair. On y ajoute donc un contrôle d'intégrité (parce que le XOR c'est pas ouf niveau intégrité) ==> un Tag définit qui dépend de la clef (donc un MAC) ### Comment évaluer la sécurité d’un chiffrement ? Sans information à propos de la clef, le chiffré ne doit pas faire fuiter d’information à propos du message. Avec la méthode naïve qu’on a expliqué précédemment, comme elle est déterministe, pour un clair on a un chiffré, donc si le clair se répète on reverra le même chiffré. 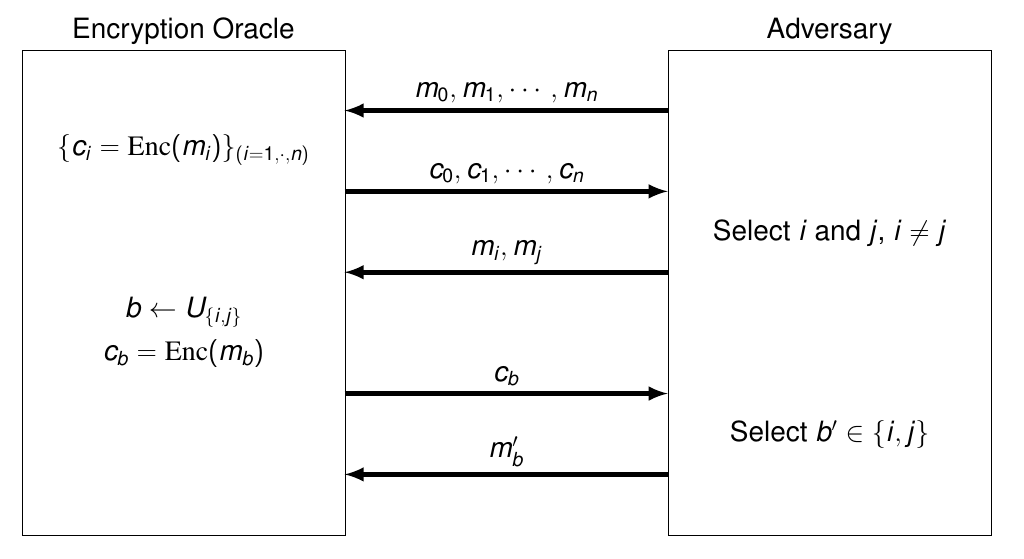On va jouer à un “jeu d’indistinguabilité  (m0, Enc(m0)) ; (m1, Enc(m1)) **;** (m2, Enc(m2)) - IND-KPA (Known Plaintext Attack): Adversary sees pairs ($m_i, Enc(m_i)$) - Clair Connu - Oracle de chiffrement - IND-CPA (Chosen Plaintext Attack): adversary SELECTS messages $m_i$ and ASKS an entity to encrypt $m_i$ - Il choisit des messages, il en reçoit les chiffrés, il sait les reconnaître - Oracle de chiffrement - IND-CCA (More information during asymmetric encryption lesson) - Chosen Ciphertext Attack - Celui-là c’est le standard d’indistinguabilité - Oracle de déchiffrement - CCA utilisable surtout avec du chiffrement asymétrique Dans le cadre de IND-CPA, le mode d’opération ECB n’est pas sécurisé au sens théorique, car $A_{cpa} = \frac{1}{2}$, il ne doit donc pas être utilisé en pratique. **Cas ECB** On connaît la correspondance vu que c'est déterministe ==> fail **Cas de CBC** Si l'IV (vecteur d'initialisation) est nul, réinitialisé au début de chauqe chiffrement ou qu'il est la sortie du précédent on peut trouver des techniques pour déterminer. l’IV est généré à partir du secret partagé (de la même manière que la clef symétrique) L’IV doit être unique, aléatoire mais prédictible ### Dans la pratique **Mode utilisé** Depuis TLS v1.3 on utilise plus CBC, on utilise GCM. CBC n’est plus utilisé en pratique **Philosophie du chiffrement symétrique moderne** S’éloigner du chiffrement parfaitement sûr (et donc de ses contraintes) mais de manière contrôlée (avec un niveau de sécurité) // maybe insérer un truc sur  Dans la joie et la bonne humeur : [le prochain cours !](https://notes.ar-lacroix.fr/s/1OJ0EQaTY#)